山村・Fazekas 研究室の今野咲彩さん(M2)、田口輝希さん(M1)、黄新昊さん(M1)、深浦晴輝さん(B4)が、2022年2月16,17,18日に京都大学数理解析研究所で開催された研究集会「論理・代数系・言語と計算機科学の周辺領域」にて研究発表を行いました。
それぞれの研究成果を発表し、他大学の研究者とともに意見交換を行いました。
今野咲彩さんは、「Left simple and left cancellative semigroups without idempotents」のタイトルで英語で発表を行いました。
発表の概略:
Left simpleでleft cancellative(right simpleかつright cancellative)な半群の構造はまだ明らかになっていないという事実を受け、その性質を持つ半群を構成しました。全射で任意の逆像の濃度が無限濃度となる写像を元とするidempotentを持たない半群を構成し、それがLeft simpleでleft cancellativeであることを発表しました。1932年にR.BaerとF.Leviが、単射の写像を元とするidempotentを持たない半群(Baer-Levi半群)を構成しており、それと同型であるかどうかの確認が現在直面している困難となっています。
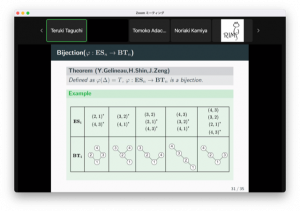
田口輝希さんは、「Correspondence between down-up alternating permutations and increasing 1-2 trees」のタイトルで発表を行いました。
発表の概略:
encoding sequenceを用いたdown-up alternating permutationとincreasing 1-2 treeの対応関係の証明や具体例、アルゴリズムを、Euler number、Entringer number、Entringer familyとの関係を交えつつ紹介した。また、そこから発展するこれからの研究目標も紹介した。
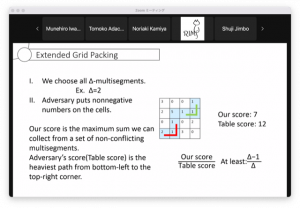
黄新昊さんは、「Slightly Improved Dynamic Algorithm for LIS」のタイトルで発表を行いました。
発表の概略:
今回のRIMSで最長増加部分列に対する近似アルゴリズムをテーマに発表しました。LIS問題とDynamic Settingの定義から、既存の近似アルゴリズムと近似問題Extended Grid Packing問題を紹介し、新たな近似度が高い方法を導入しました。そして、再帰的データ構造を用いてLISの近似解を計算します。これからは、新しい方法についてのUpdate Timeなどを確認して、アルゴリズムを練り直します。
深浦晴輝さんは、「Diagrams over groups and small cancellation conditions」のタイトルで発表を行いました。
発表の概略:
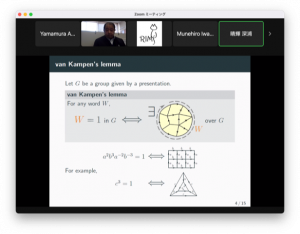
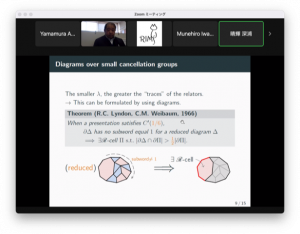
発表の内容は、Ol’shanskii著, Geometry of Defining Relations in Groupsの最初の方をまとめたものである。最初に帰結の導出の可視化であるdiagramの例を挙げて定義を述べたあと、帰結とdiagram の対応を述べたvan Kampenの補題を紹介した。次に表示の制限であるスモールキャンセル条件を導入し、それがdiagramにどう作用するかを説明し、ある程度強い条件満たすときのdiagramの特徴を述べた定理の証明を簡単に紹介した。最後に群のword problemを紹介し、スモールキャンセル群のword problemを解くDehnのアルゴリズムを構成した。
参加・研究発表の感想:
今野咲彩
私は学会で数学の内容を発表したことは初めてで、研究者の方々に向かって発表するのはとても緊張しました。毎日の活動では現在直面している困難にばかり目を向けていましたが、発表を通して研究の出発点に目を向ける必要性を感じました。そもそもなぜLeft simpleでleft cancellativeな半群の構造は研究されてこなかったのか、構成したものは予想と照らしてどうだったのか、idempotentがあるとどうなるのかなどの質問を受けました。研究の土台や基礎の部分に目を向けて修士論文を書き上げたいと思いました。発表者の中で、自分が留学に行った際にお世話になった先生や、秋田に留学しに来ていた方もおり、研究集会の中で交流ができたことや、半群論に関する研究発表を聞いて理解できる部分があったことは嬉しかったです。
田口輝希
発表した感想としては、初めての研究発表、それもオンラインということで、スライドの準備や表現、時間の調整や発表練習もとても大変で本番も緊張したが、いい経験になった。発表時間に対し内容を詰め込みすぎてしまったので、次回の研究発表の際はその点に気を付けたい。他の発表者の講演を聞いた感想については、自分の理解できる内容、複雑な内容等様々だったが、全体を通して発表そのものの流れやスライドの作り方などの参考になる部分が多く、これからの発表で取り入れていきたいと思った。今回は日本語での発表になったが、英語での言い回しや表現を学び、次回は英語で発表ができるように努力したいと思う。
黄新昊
初めてRIMS共同研究に参加しましたので、論理・代数系の発表を伺うことができ、大変勉強になった。この発表を通して、限られた時間の中で自身の研究成果を他者に分かりやすく説明することの難しさを実感することができ、とても良い経験になったと思います。また、他の人の発表や質問からで自分にはない考えを得ることができたことも、見つかったことも大きな成果だったと思います。
今後ともこの貴重な場に参加できるよう研究に励み、自分の説明能力を上昇し、そして、様々な考えや意見をいただいたことが発表会での大きな収穫でありました。
深浦晴輝
今回の発表は自分にとって初めての学術発表であり、大変多くのことを学ばせていただきました。発表後、スライド内の図について質問を頂きました。図の制作には力を入れていたので、触れていただけて嬉しかったです。同じ本を読んだという方からは、より深い内容で補足のコメントを頂き、非常に勉強になりました。他の方の発表では、数名がword problemについて触れていました。自分が学んでいる内容が実際に有名なものであることが実感でき、全く異なるアプローチを知ることができて理解を深めることができました。今読んでいる本の内容を今後研究していく上で、大きなモチベーションとなりました。今回、このような貴重な体験をさせていただけたことを感謝しております。