専門分野
位相幾何学,多様体間の写像の理論,大域的特異点論,投影による形状理解,科学教育
- 写像による形状理解の基礎理論と応用
- 初学者や社会人の学び直しのための数学教材の開発
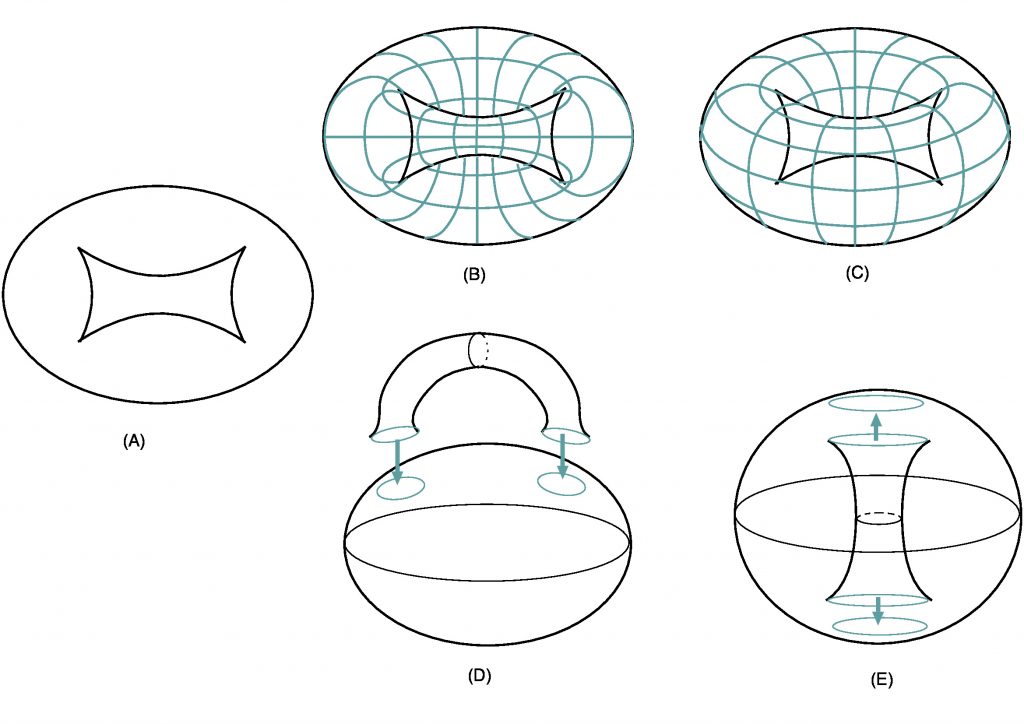
図1(A) は,トーラス(ドーナツの表面)を線で表現したもので,図1(B), (C)は,トーラスを紙の上に投影する2タイプの方法を,図1(A)に補助線を描き加えて表現したものです。図1(A)の線は輪郭線と呼ばれます(実際には,一部は隠れて見えない)。
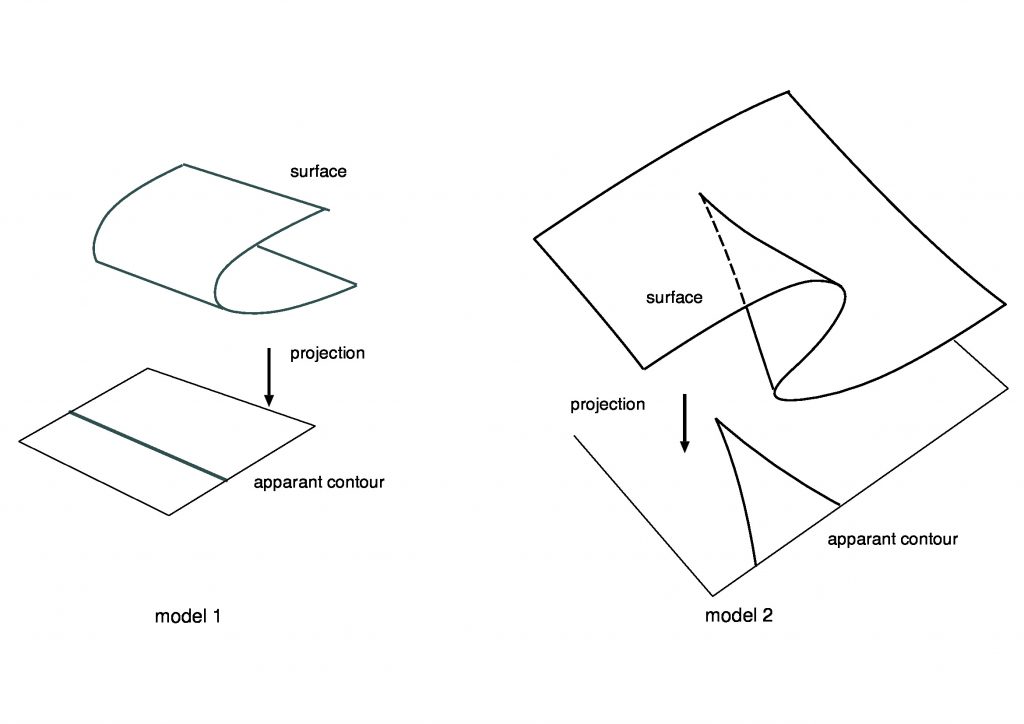
輪郭線は実は2次関数 $x^2$ の極値を連ねたもので,ところどころにある尖りは,3次関数 $x^3 − 3ux$ の極値の数が $u$ により変化することで発生します(Whitneyの定理, 図2)。この原理をもとに輪郭線から曲面のかたちを推測することは,ロボット視覚の研究に繋がりそうです。
この原理を一般化すると(Whitney, Thom, Mather,…,写像の特異点理論) ,目に見えない高次元のかたち(多様体)をも,投影と輪郭線を手がかりに推測することもできそうです。
たとえば, $S^2 \times S^2$ , $S^2 \tilde{\times} S^2$ (Hirzebruch の複素曲面)という4次元多様体は,ちょうどこの図と同じ輪郭線を持ちます。図1(A)のトーラスの輪郭線は,球面に把手(とって)を付けたことを表現していますが(図1(D),(E)),Hirzebruch の複素曲面も同じく,4次元球面に把手を付けたものだということが,この輪郭線から分かります。
高次元になると,投影で失われる情報も多いのですが,それでも輪郭線は,かたち(多様体)について何かを伝えています。ときには失われた情報のいくつかを加えて様子を見ながら,輪郭線がかたちについて何を伝えているのかを探るのが,輪郭線による形状理解という研究です。
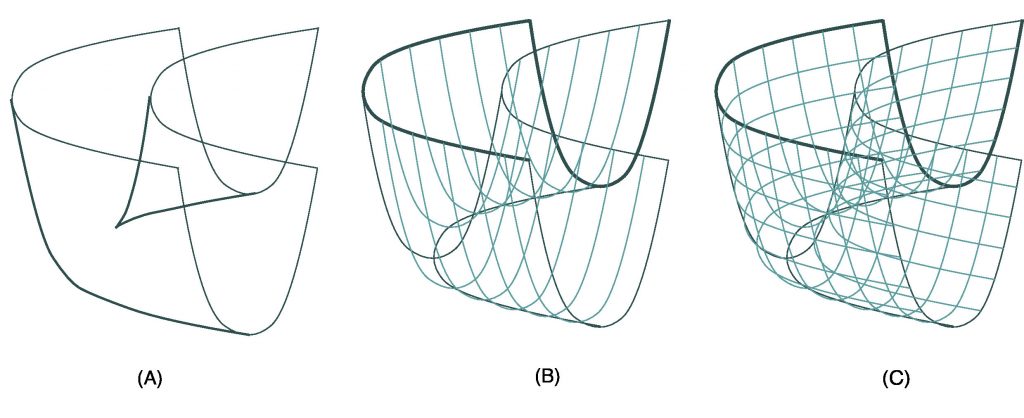
図3(B),(C)は,放物線を放物線に沿ってスライドさせたものです。このとき,図3(A)のような尖った点を1つもつ独特な包絡線が現れます。
絵から見て取れるように,この線は「カーブしたU字型の溝」がつくる輪郭線ですが,同時にハンカチを4つ折りにしたときの輪郭線とも捉えられます。
実は,この輪郭線は a+b次元の「紙」 $D^a \times D^b$ が4つ折りされたことを示す証拠で,高次元のかたち(多様体)の輪郭線の重要な構成部品と思われ,cusped fan と呼んで研究しています(弘前大学山本稔先生との共同研究)。ここにも2次元の様子から高次元を探るという例が見られます。
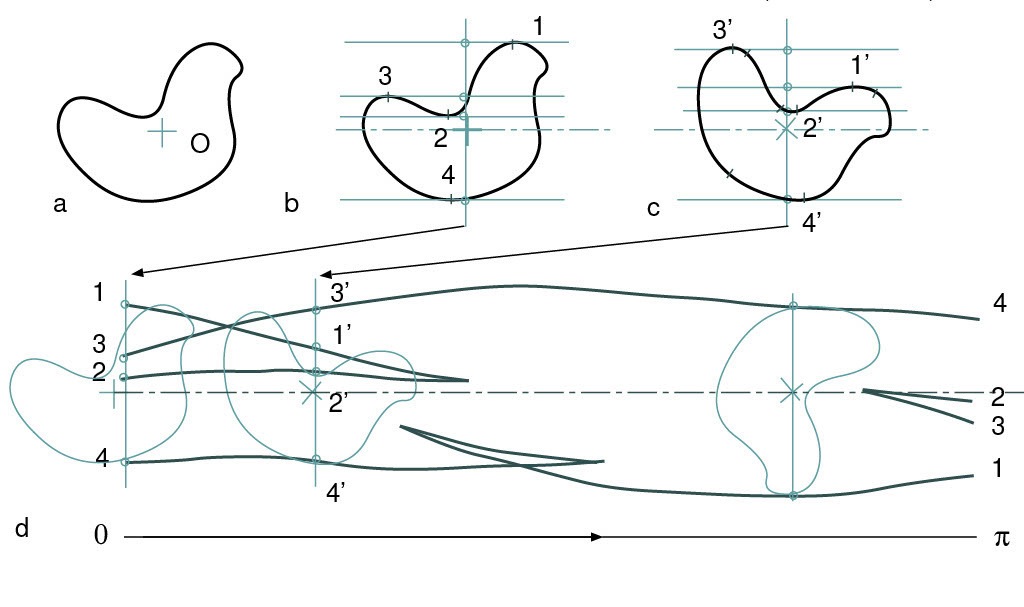
投影を利用してかたちを探る道具として,「パノラマビュウ」を考えました。図4にある図形a(鳩型)を,b,c のように,つぎつぎと角度を変えて直線に投影し,輪郭「点」を集めると(こんどは線に投影するので,輪郭は線ではなく点になる),dのような,ところどころに尖った点をもつ線が出現します。これは,実はメビウスの帯に描かれた曲線ですが,この線から,原図形の変曲点,くぼみや原図形の周囲長など,かたちの特徴を知ることができます。パノラマビュウを用いると,平面閉曲線についての,ファブリシウス-ビエレの定理,バンチョフの定理,コーシー-クロフトンの定理などの別証明が得られます(北海学園大学佐野貴志,弘前大学山本稔先生との共同研究)。
- 方程式の解,例えば $x^3 − y^2 − c = 0$ を満たす複素数 $x$, $y$ がつくる4次元空間内の曲面のかたちを,実部への投影を使って探る(大学院生との研究)
- $P^2$ (射影平面)は3次元空間に住めない曲面の最も基本的な例であるが,その古典的3次元モデル(Steiner曲面,Boy曲面)の理解と再構築を行う(大学院生との研究)
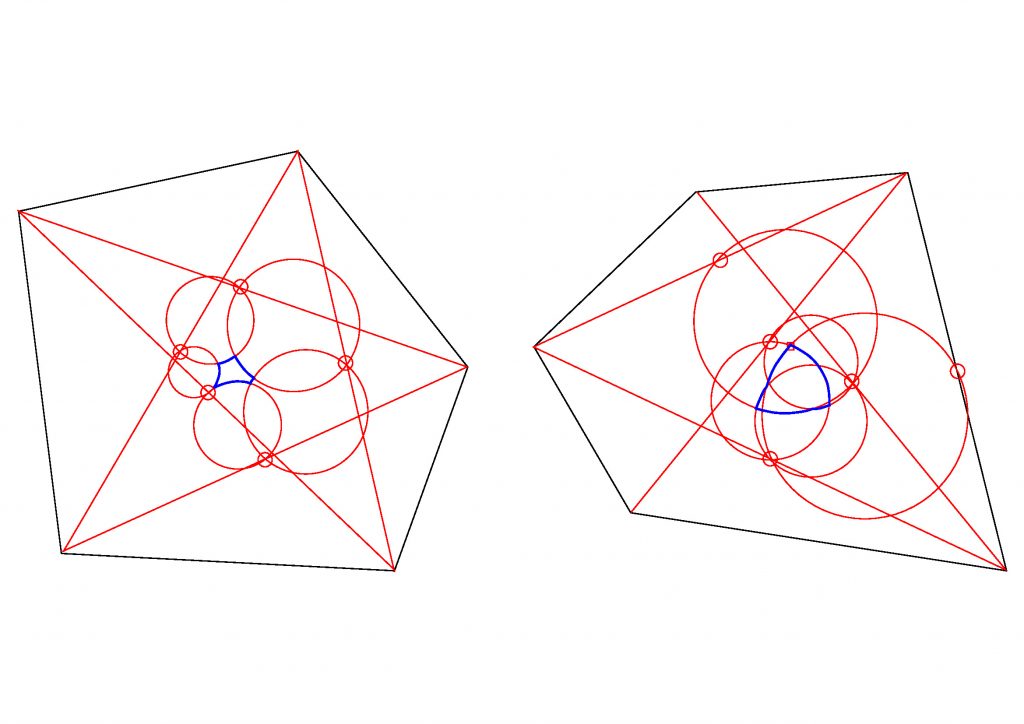
- 多角形の中心を軌跡として捉え,どんな形状の軌跡が現れるのか,また,軌跡をもとに凸多角形の形状分類ができるかを考える(4年生との研究)。図5は,5角形の中心の軌跡の作図を示している。中央の線が中心の軌跡で,軌跡の囲む領域の大きさや膨らみ方が大きく異なることがわかる
数学,幾何学の考え方が随所に使われます。
- 色彩情報を利用した地上撮影の雲画像による天候判断
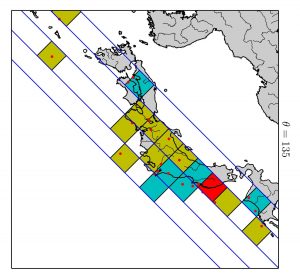
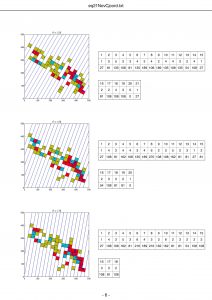
- 日本列島で発生した地震震央の直線状配置の検出(図7,8)
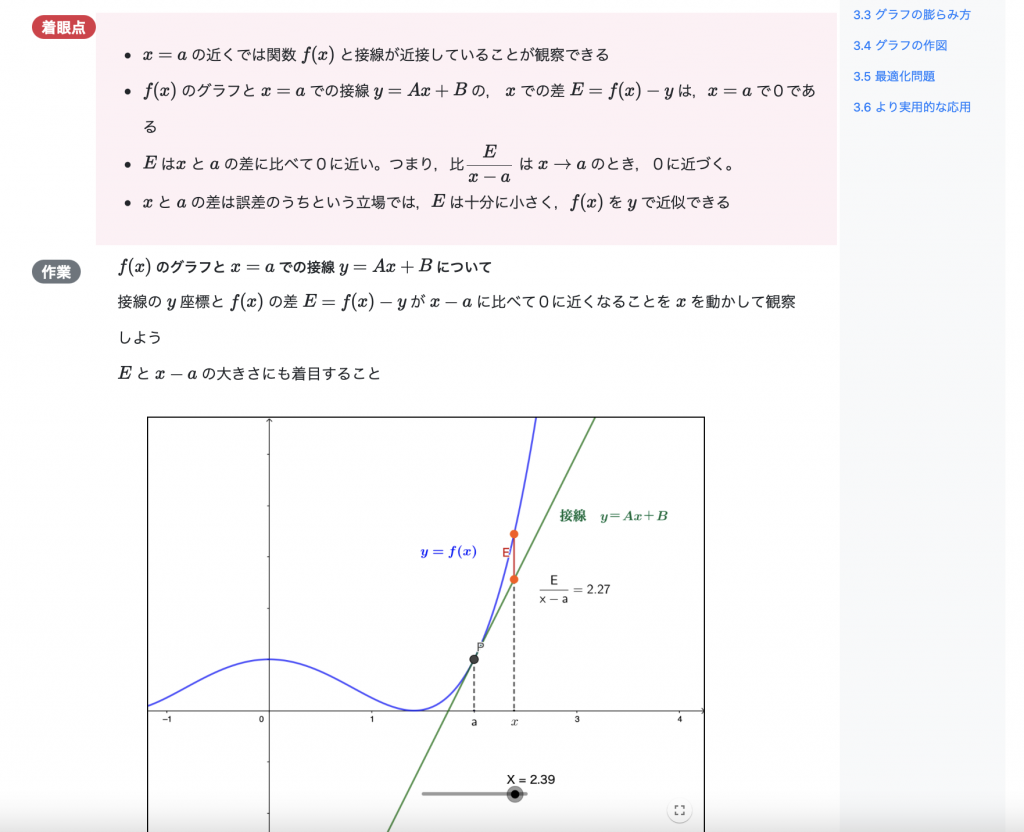
実際の課題や他分野の研究で数学を活用するためには,基本的な概念を自分で何度も体験しながら,実例や他の概念と関連づけて理解することが大切です。このような学習を助けるためのウェブ教材を作成しています(図6,秋田大学横山洋之,弘前大学山本稔,聖霊女子短期大学小林弥生先生との共同開発)。
高大接続教育部門員として,高等学校で数学を身近に感じ,考える楽しさを体験してもらう授業(アカデミック授業)や,在学生に対する質問教室,テキストの編集や作成を行っています。
https://www.akita-u.ac.jp/kdcenter/