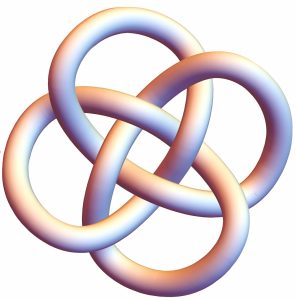中江康晴（数理科学コース教員）の研究紹介

研究テーマ：３次元多様体の位相的性質

数学には大きく代数・解析・幾何・応用数理の４つの分野があります。私は幾何学分野で、特にトポロジーと呼ばれる柔らかい幾何学の研究を行っています。

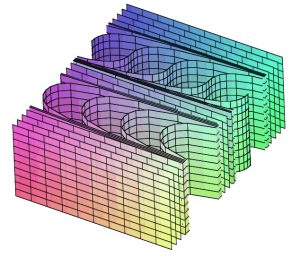
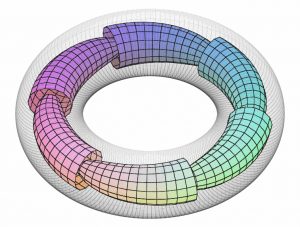
研究対象となるのは、３次元の図形である３次元多様体です。この３次元多様体の中に、１次元（直線や曲線）や２次元（平面や曲面）を敷き詰めたような「葉層構造」を用いて、３次元多様体のトポロジーとしての性質を研究しています（図１）。特に、図のような「レーブ葉層構造」（図２）を部分的に持たないような葉層構造で、トート葉層構造と呼ばれるものに関心があります。

テーマ１：結び目に沿ったデーン手術で得られる３次元多様体の性質

結び目とは３次元の中に埋め込まれた円周のことをいいます（図３）。この結び目を太らせて取り除いて、取り除いたところにまた別の太らせた円周を貼り付けると、貼り付け方によって、さまざまな３次元多様体を作ることができます。このような操作をデーン手術といいます。

全ての閉３次元多様体は、結び目や絡み目（結び目が複数絡まったもの）に沿ったデーン手術で得られることが知られています。

特に私は、結び目に沿ったデーン手術で得られる３次元多様体に、トート葉層構造と呼ばれる葉層構造が存在するかどうか、またさらにその３次元多様体の基本群が左順序付け可能という性質をもつかどうかについて研究を行っています。

テーマ２：アノソフ流を用いた３次元多様体の性質の研究

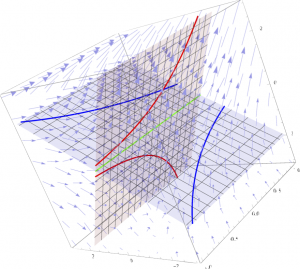
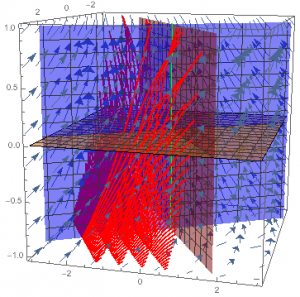
空間の中の各点に方向を定めたものを、ベクトル場といいます。ベクトル場に沿って進む方向を辿ると、空間の中の「流れ」ができます。この「流れ（フロー）」のうち、流れる方向に垂直な２方向が、流れに沿って縮む方向と伸びる方向があるような流れを「アノソフ流」と呼びます（図４）。

アノソフ流の方向と縮む方向、またアノソフ流と伸びる方向をそれぞれ合わせると２次元の平面が定まり、それらの平面たちに沿うような曲面を集めると、３次元空間内の２つの葉層構造（安定葉層と不安定葉層）が得られます（図５（１）と（２））。

これら２つの葉層構造が、R-coveredという性質を持つものに着目して研究を行っています。